Backdoor Trigger Restoration
Published:
This is my on-going project only for demonstration, advised by Prof. Ting Wang at PSU.
Introduction
This is a project diverged from Backdoor Certification, you may first want to read that.
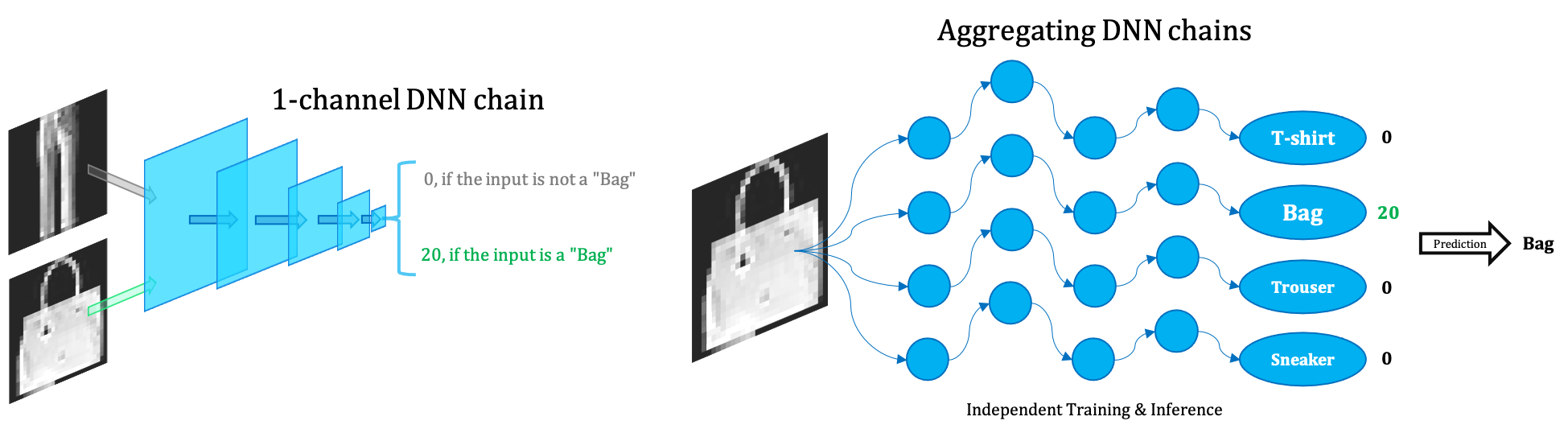
Backdoors within DNN models are dangerous, and an important line of work focus on detecting these potential backdoors. Some of these detection methods (e.g. Neural Cleanse) first reverse engineer (restore) the potential backdoor, then utilize anomaly detaction to tell if there is indeed a backdoor.
We propose an efficient heuristic algorithm that focuses on restoring the potential backdoor trigger in a given DNN. Our algorithm requires NO or very few clean inputs, while supporting both perturbation triggers (add the pattern to an image) and patch triggers (stamp a pattern onto an image). Our restored triggers reach high ASR and match the real trigger well.
Method
Intuitively, for a batch of $N$ inputs, searching for the potential backdoor trigger is similar to the following optimization:
\[\text{trigger} = \text{argmin}_{r} \sum_{i=1}^N \Big(f_{source}(x_i + r) - f_{target}(x_i + r)\Big)\]Nevertheless, directly optimizing the equation by Stochastic Gradient Descent is empirically difficult. As shown in the three following figures, the gradient information (orange) could be quite noisy:
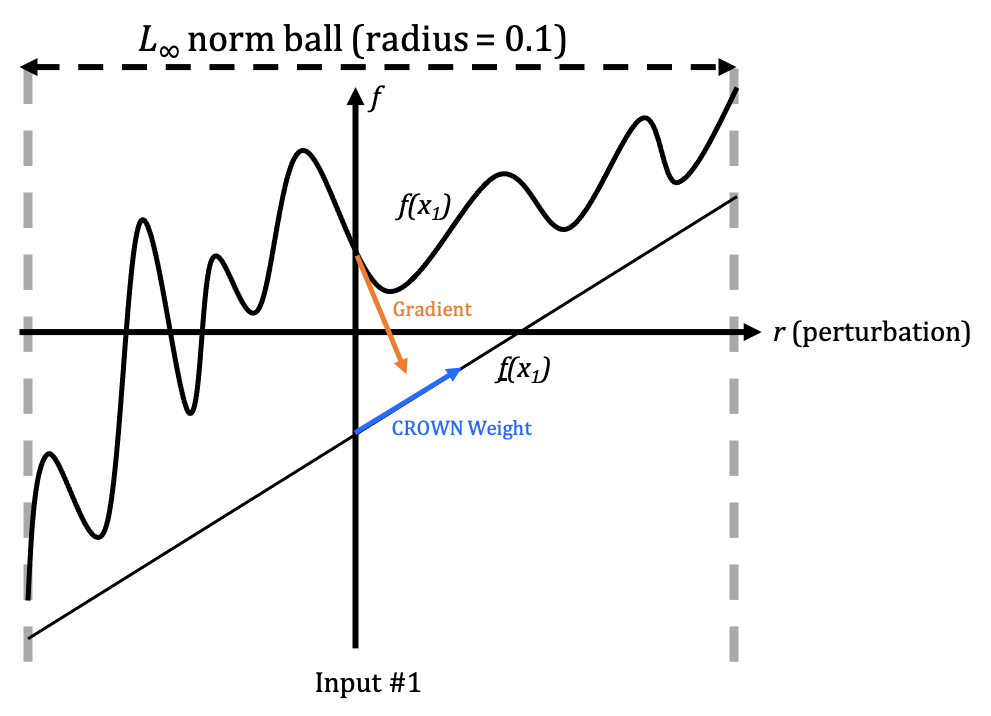
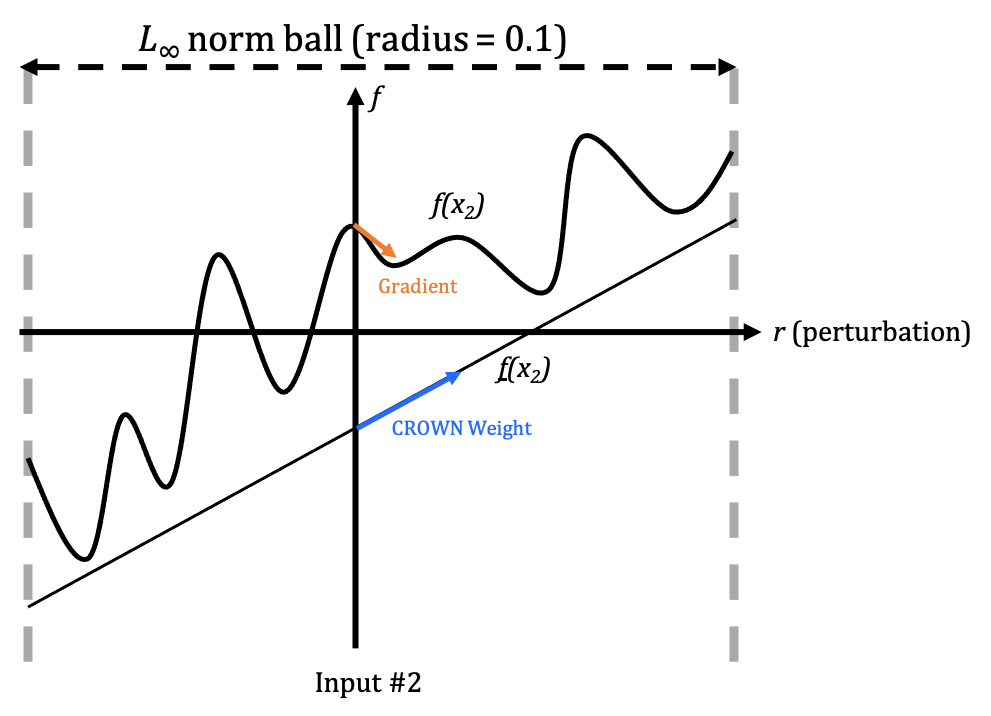
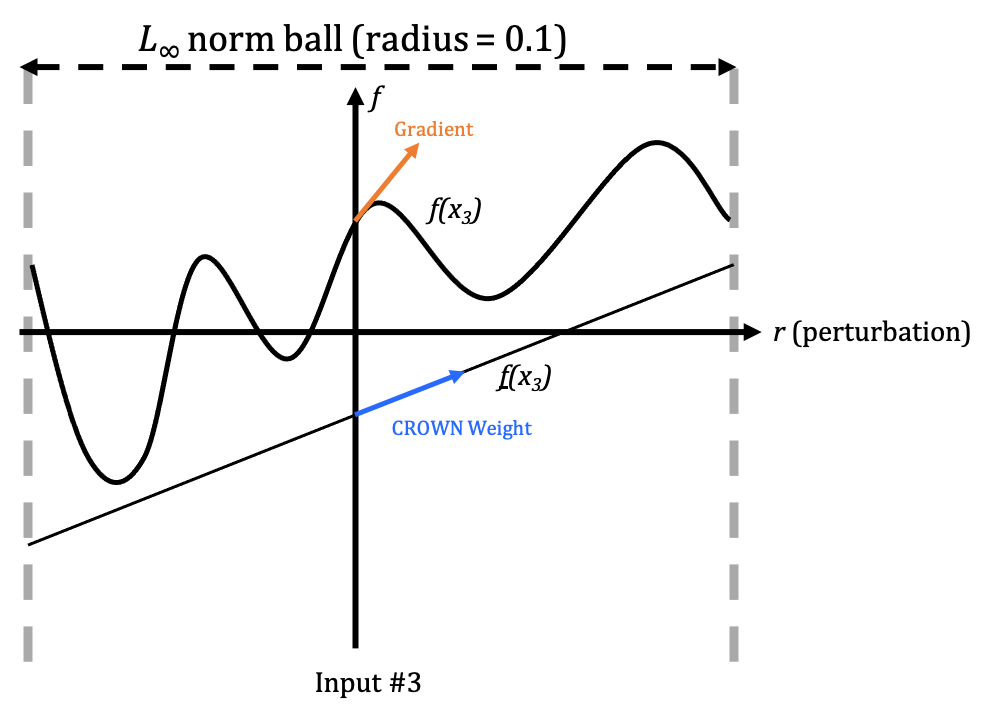
Remember that CROWN relaxes NN to linear function, and as shown in the figures above, we may view the CROWN weight for each input dimension (blue) as an “approximate gradient” in a certain vicinity. And this “approximate gradient” is usually less noisy.
So we simply replace the exact gradients with the “approximate gradients”:
\[\mathbf r_{t+1} = \mathbf r_t - \text{lr} * \sum_{i=1}^N \nabla_{\mathbf x,approx} f(\mathbf x_i + \mathbf r_t)\]This makes the optimization (restoring or searching for triggers) much easier, and our experiments have confirmed this.
Results
Some restoration results:

- I’m still refining both the idea and experiments.