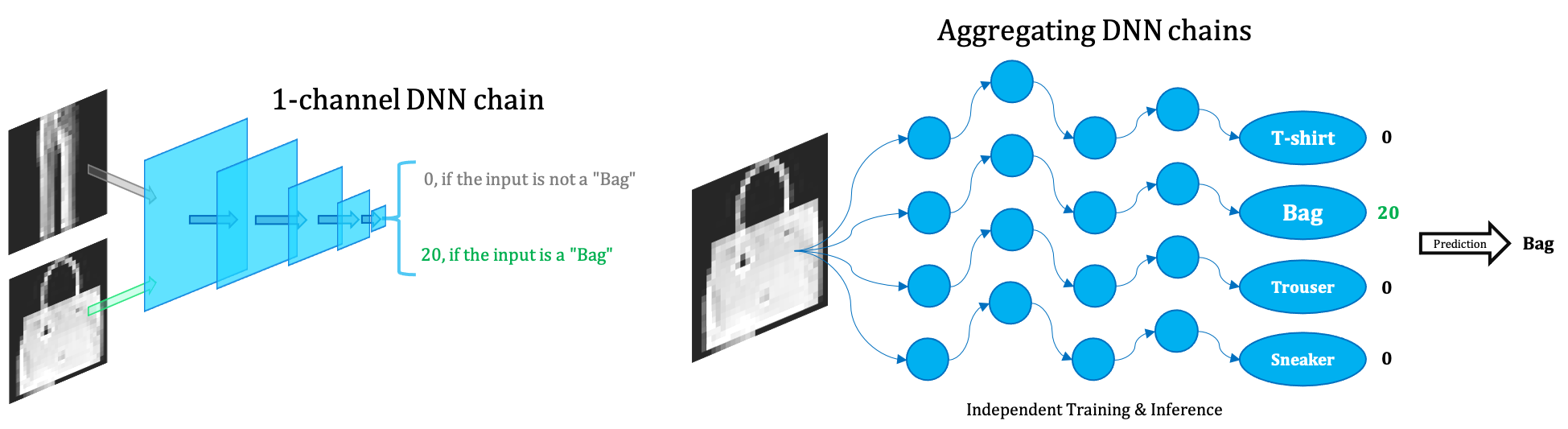
Backdoor Certification
Published:
This is my on-going project only for demonstration, advised by Prof. Ting Wang at PSU.
Introduction
In the field of DNN security, adversarial attacks and backdoor attacks are the typical ones.
- Adversarial Attack: For a given input, the attacker adds an imperceptible noise(perturbation), leading to the DNN misclassifying the perturbed input; The adversarial perturbation is input-spcific, and usually obtained via PGD.
- Backdoor Attack: For all inputs, the attacker stamped a trigger pattern to them, leading to the DNN misclassifying all the stamped input; There are a variety of trigger types and implantation strategies, and backdoors are usually injected via data poisoning at training stage.
Certified robustness has been widely discussed, to end the arm race between adversarial attacks and defenses. We aim at taking the first step by introducing certification to stop the arm race of backdoor attacks and defenses.
Method
We first formulate the backdoor certification problem; No (perturbation-)backdoor exists in a norm ball $S$ can be expressed as the inequation:
\[\min_{r\in S}\max_i f_{source}(x_i + r) - f_{target}(x_i + r) > 0\]We base our work on an existing NN verifier, CROWN (LiRPA). As shown in the following figure, CROWN would relax the non-convex NN function $f$ into a linear function $\underline f$ w.r.t. the input dimensions, where $f(x + r) \ge \underline f(x + r)$ for any $r\in S$.

We use the lower bound linear function for certifying backdoor:
\[\min_{r\in S}\max_i \underline f_{source}(x_i + r) - \overline f_{target}(x_i + r) > 0\]Notice that (2) naturally yields a sufficient condition for (1). The following figure shows our backdoor certification process:
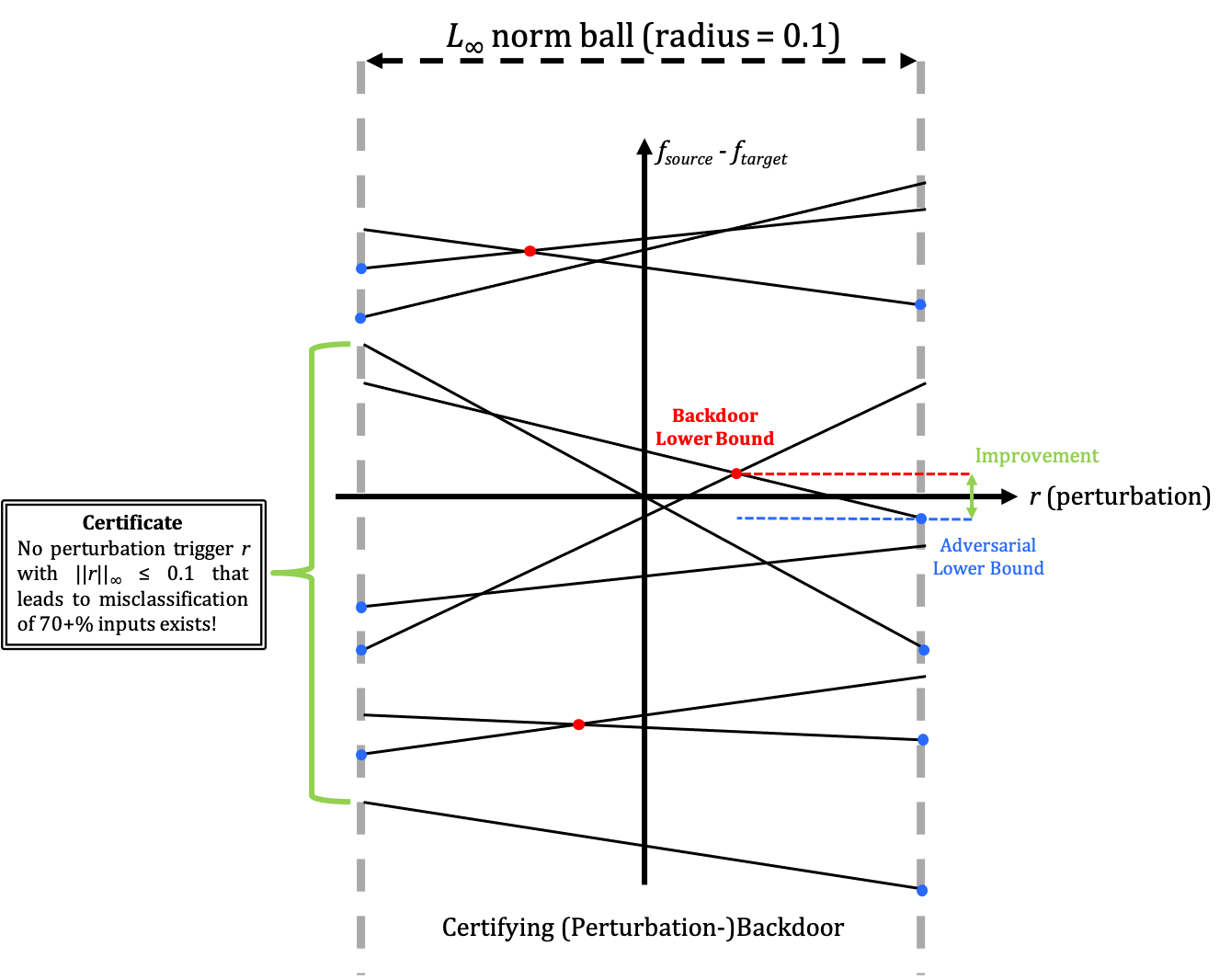
Each solid line corresponds to the linear relaxation $\underline f_{source}(x_i + r) - \overline f_{target}(x_i + r)$ of the NN given input $x_i$. After grouping the inputs, we are able to give a certification like: There is no perturbation trigger $r \in S$ that would lead to $\rho\%$ inputs being misclassified.
We could further introduce optimization, Bound and Branch to tighten the bounds.
Results
A metric for certified adversarial robustness is the $\textit{adversarial-attack-free radius}$, under which it’s impossible to perform adversarial attack. Likewise, we extend the metric to $\textit{backdoor-free radius}$ under which it’s impossible to perform backdoor attack.
Obviously: \(\textit{adversarial-attack-free radius} \le \textit{backdoor-free radius}\) and our initial experiment results show that for the same NN, there could be $>15\%$ improvement/gap between the two radius.
- I am still refinining the experiments.